Answer:
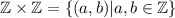
Explanation:
In general, the Cartesian product of two sets
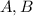 is a new set defined by
is a new set defined by
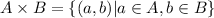
The pair
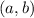 is ordered pair because the order is important, that is to say, in general
is ordered pair because the order is important, that is to say, in general
 .
.
One of the most important Cartesian products in mathematics is
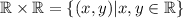 which is precisely the Cartesian Plane xy. The set
which is precisely the Cartesian Plane xy. The set
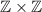 is a subset of
is a subset of
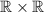 which is the set of all the points in the Cartesian plane whose coordinates are integers numbers. So, sketching the set
which is the set of all the points in the Cartesian plane whose coordinates are integers numbers. So, sketching the set
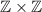 we have a picture as the shown below.
we have a picture as the shown below.