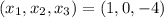Question

Solve the system of linear equations using the Gauss-Jordan elimination method. 2x1 − x2 + 3x3 = −10 x1 − 2x2 + x3 = −3 x1 − 5x2 + 2x3 = −7 (x1, x2, x3) =

Answer 1

The solution is:
`(x_(1), x_(2), x_(3)) = (1,0,-4)`

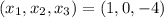
Explanation:

The Gauss-Jordan elimination method is done by transforming the system's augmented matrix into reduced row-echelon form by means of row operations.

We have the following system:

`2x_(1) - x_(2) + 3x_(3) = -10`

`x_(1) - 2x_(2) + x_(3) = -3`

`x_(1) - 5x_(2) + 2x_(3) = -7`

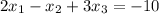
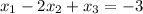
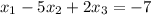
This system has the following augmented matrix:

`\left[\begin{array}{ccc}2&-1&3|-10\\1&-2&1|-3\\1&-5&2| -7\end{array}\right]`

To make the reductions easier, i am going to swap the first two lines. So

`L1 <-> L2`

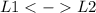
Now the matrix is:

`\left[\begin{array}{ccc}1&-2&1|-3\\2&-1&3|-10\\1&-5&2| -7\end{array}\right]`

Now we reduce the first row, doing the following operations

`L2 = L2 - 2L1`

`L3 = L3 - L1`

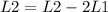
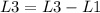
So, the matrix is:

`\left[\begin{array}{ccc}1&-2&1|-3\\0&3&1|-4\\0&-3&1| -4\end{array}\right]`

Now we divide L2 by 3

`L2 = (L2)/(3)`

So we have

`\left[\begin{array}{ccc}1&-2&1|-3\\0&1&(1)/(3)|(-4)/(3)\\0&-3&1| -4\end{array}\right]`

Now we have:

`L3 = 3L2 + L3`

So, now we have our row reduced matrix:

`\left[\begin{array}{ccc}1&-2&1|-3\\0&1&(1)/(3)|(-4)/(3)\\0&0&2| -8\end{array}\right]`

We start from the bottom line, where we have:

`2x_(3) = -8`

`x_(3) = (-8)/(2)`

`x_(3) = -4`

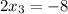
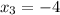
At second line:

`x_(2) + (x_(3))/(3) = (-4)/(3)`

`x_(2) - (4)/(3) = -(4)/(3)`

`x_(2) = 0`

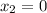
At the first line

`x_(1) -2x_(2) + x_(3) = -3`

`x_(1) - 4 = -3`

`x_(1) = 1`

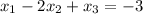
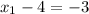
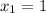
The solution is:
`(x_(1), x_(2), x_(3)) = (1,0,-4)`