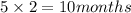Question

A population of rabbits triples every 2 months If there are 2 rabbits initially, how long will it take for the population to increase to 500 rabbits? Round your answer to the nearest whole number (5 marks)

Answer 1

The rabbit population will reach 500 after 10 months.

Step-by-step explanation:

According to the given data:

The initial number of rabbit's equals 2.

Number of rabbit's after 2 months =2x3= 6

Number of rabbit's after 4 months = 6x3=18

Number of rabbit's after 6 months = 18x3=54

Number of rabbit's after 8 months = 54x3=162

Thus we can see that the number of rabbit's form a Geometric series with common ratio =3 and initial term = 2

Now the general term of a geometric series with first term 'a' and common ratio 'r' is given by

`T_(n+1)=ar^(n)`

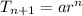
Thus we need to find when the term becomes 500 thus using the given data we have

`500=2\cdot 3^(n)\\\\3^(n)=250\\\\(n)log_3(3)=log_3(250)\\\\(n)=5.025\\\\`

Thus the fifth term (excluding the start term) will have a rabbit count of 500 now since each term has a time difference of 2 months thus sixth term will occur after
`5* 2=10months`