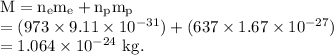Question

A system of 1610 particles, each of which is either an electron or a proton, has a net charge of −5.376×10^−17 C. How many electrons are in this system? What is the mass of this system?

Answer 1

Number of electrons in the system = 973.

Total mass of the system =
`\rm 1.064* 10^(-24)\ kg.`

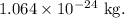
Step-by-step explanation:

Assumptions:

• 
  `\rm n_e` = number of electrons in the system.

• 
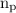  `\rm n_p` = number of protons in the system.
• 
  `\rm q_e` = charge on an electron =
  `\rm -1.6* 10^(-19)\ C.`

• 
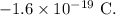
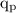  `\rm q_p` = charge on a proton =
  `\rm +1.6* 10^(-19)\ C.`

• 
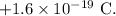
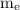  `\rm m_e` = mass of an electron =
  `\rm 9.11* 10^(-31)\ kg.`

• 
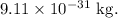
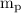  `\rm m_p` = mass of a proton =
  `\rm 1.67* 10^(-27)\ kg.`

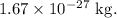
Given:

• Total number of particles in the system, N = 1610.
• Net charge on the system, q =
  `\rm -5.376* 10^(-17)\ C.`

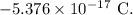
Since, the system is comprised of electrons and protons only, therefore,

`\rm N = n_e+n_p\\n_p=N-n_e\ \ \ \ \ \ ................\ (1).`

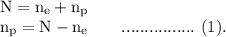
The net charge on the system can be written in terms of charges on electrons and protons as

`\rm q=n_eq_e+n_pq_p\ \ \ \ \ ...................\ (2).`

Putting the value of (2) in (1), we get,

`\rm q=n_eq_e+(N-n_e)q_p\\q=n_eq_e+Nq_p-n_eq_p\\q=n_e(q_e-q_p)+Nq_p\\n_e(q_e-q_p)=q-Nq_p\\n_e=(q-Nq_p)/(q_e-q_p)\\=(-5.3756* 10^(-17)-1610* 1.6* 10^(-19))/(-1.6* 10^(-19)-1.6* 10^(-19))=972.98\\\Rightarrow n_e\approx 973\ electrons.`

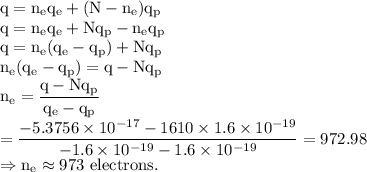
It is the number of electrons in the system.

Therefore, the number of protons is given by

`\rm n_p = N-n_e=1610-973=637.`

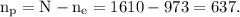
The total mass of the system is given by

`\rm M=n_em_e+n_pm_p\\=(973* 9.11* 10^(-31))+(637* 1.67* 10^(-27))\\=1.064* 10^(-24)\ kg.`