Question

What is the energy stored between 2 Carbon nuclei that are 1.00 nm apart from each other? HINT: Carbon nuclei have 6 protons and 1.00 nm = 1.00x10^-9m

A. 8.29x10^-18J
B. 2.30x10^-19J
C. 8.29x10^-10J
D. 8.29x10^-9J
E. 0 J

Answer 1

`A. 8.29* 10^(-18)\ J`

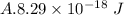
Step-by-step explanation:

Given that:

p = magnitude of charge on a proton =
`1.6* 10^(-19)\ C`

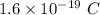
k = Boltzmann constant =
`9* 10^(9)\ Nm^2/C^2`

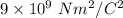
r = distance between the two carbon nuclei = 1.00 nm =
`1.00* 10^(-9)\ m`

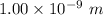
Since a carbon nucleus contains 6 protons.

So, charge on a carbon nucleus is
`q = 6p=6* 1.6* 10^(-19)\ C=9.6* 10^(-19)\ C`

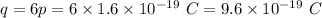
We know that the electric potential energy between two charges q and Q separated by a distance r is given by:

`U = (kQq)/(r)`

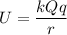
So, the potential energy between the two nuclei of carbon is as below:

`U= (kqq)/(r)\\\Rightarrow U = (kq^2)/(r)\\\Rightarrow U = (9*10^9* (9.6* 10^(-19))^2)/(1.0* 10^(-9))\\\Rightarrow U =8.29* 10^(-18)\ J`

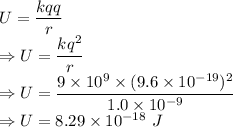
Hence, the energy stored between two nuclei of carbon is
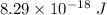`8.29* 10^(-18)\ J`.