Question

Use the "rule of 72" to estimate the doubling time (in years) for the interest rate, and then calculate it exactly. (Round your answers to two decimal places.) 7.7% compounded weekly.

"rule of 72" yr

exact answer yr

Answer 1

Using the rule of 72, the doubling time is 9.35 years.

The exact answer is that the doubling time is 8.89 years.

Explanation:

By the rule of 72, we have that the doubling time D is given by:

`D = (72)/(Interest Rate)`

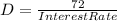
The interest rate is in %.

In our exercise, the interest rate is 7.7%. So, by the rule of 72:

`D = (72)/(7.7) = 9.35`.

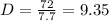Exact answer:

The exact answer is going to be found using the compound interest formula(since the rule of 72 is a simplification of this formula).

The compound interest formula is given by:

`A = P(1 + (r)/(n))^(nt)`

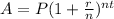
Where A is the amount of money, P is the principal(the initial sum of money), r is the interest rate(as a decimal value), n is the number of times that interest is compounded per unit t and t is the time the money is invested or borrowed for.

So, for this exercise, we have:

We want to find the doubling time, that is, the time in which the amount is double the initial amount, double the principal.

`A = 2P`

`r = 0.077`

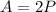
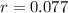
There are 52 weeks in a year, so
`n = 52`

`A = P(1 + (r)/(n))^(nt)`

`2P = P(1 + (0.077)/(52))^(52t)`

`2 = (1.0015)^(52t)`

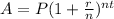
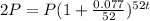
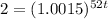
Now, we apply the following log propriety:

`\log_(a) a^(n) = n`

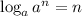
So:

`\log_(1.0015)(1.0015)^(52t) = \log_(1.0015) 2`

`52t = 462.44`

`t = (462.44)/(52)`

`t = 8.89`

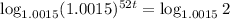
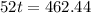
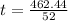
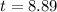
The exact answer is that the doubling time is 8.89 years.