Question

Use Gauss's approach to find the following sums (do not use formulas) a 1+2+3+4 998 b. 1+3+5 7+ 1001 a The sum of the sequence is

Answer 1

(a) 498501

(b) 251001

Explanation:

According Gauss's approach, the sum of a series is

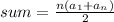`sum=(n(a_1+a_n))/(2)` .... (1)

where, n is number of terms.

(a)

The given series is

1+2+3+4+...+998

here,

`a_1=1`

`a_n=998`

`n=998`

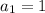
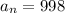
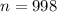
Substitute
`a_1=1`,
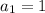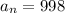`a_n=998` and
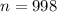`n=998` in equation (1).

`sum=(998(1+998))/(2)`

`sum=499(999)`

`sum=498501`

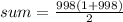
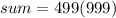
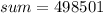
Therefore the sum of series is 498501.

(b)

The given series is

1+3+5+7+...+ 1001

The given series is the sum of dd natural numbers.

In 1001 natural numbers 500 are even numbers and 501 are odd number because alternative numbers are even.

`a_1=1`

`a_n=1001`

`n=501`

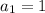
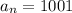
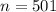
Substitute
`a_1=1`,
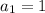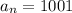`a_n=1001` and
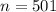`n=501` in equation (1).

`sum=(501(1+1001))/(2)`

`sum=(501(1002))/(2)`

`sum=501(501)`

`sum=251001`

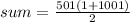
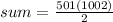
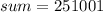
Therefore the sum of series is 251001.