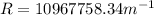Question

The spectrum from a hydrogen vapour lamp is measured and four lines in the visible light range are observed. These lines are the so-called Balmer series, where an electron makes a transition from a higher level to the second energy level (n2). In this series, the transition from n, 3 to ne 2 produces the photon with the lowest energy, this corresponds to the line with the longest wavelength. This is measured to be A 658.9 nm What value of the Rydberg constant R is obtained using these measurements? Express you answer in um to two decimal places. It is not necessary to specify the units.

Answer 1

`10942249.24 m^(-1)`

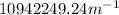
Step-by-step explanation:

Rydberg's formula is used to describe the wavelengths of the spectral lines of chemical elements similar to hydrogen, that is, with only one electron being affected by the effective nuclear charge. In this formula we can find the rydberg constant, knowing the wavelength emitted in the transcision between two energy states, we can have a value of the constant.

`(1)/(\lambda)=Z^2R((1)/(n^2_(1))-(1)/(n^_(2)^2)})`

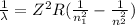
Where
`\lambda` it is the wavelength of the light emitted, R is the Rydberg constant, Z is the atomic number of the element and
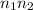`n_(1) n_(2)` are the states where
`n_(1)<n_(2)`.

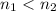In this case we have Z=1 for hydrogen, solving for R:

`R=(1)/(\lambda)*((1)/(n^2_(1))-(1)/(n^_(2)^2)})^(-1)\\R=(1)/(658.9*10^(-9)m)*((1)/(2^2)-(1)/(3^2)})^(-1)\\R=1.52*10^6m^(-1)*((36)/(5))=1.09*10^7 m^(-1)=10942249.24m^(-1)`

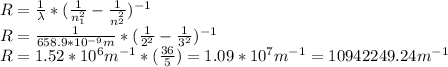
This value is quite close to the theoretical value of the constant
`R=10967758.34 m^(-1)`