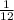Answer:
Probability of rolling a 2 and flipping a head will be
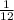
Explanation:
If we roll one die then probability to get any one side is

Therefore, probability to get 2 by rolling the die will be P(A) =

Now we flip a coin then getting head or tale probability is

Or probability to get head by flipping the coin P(B) =

Probability of happening both the events (rolling a 2 and flipping a head) will be denoted by
P(A∩B) = P(A)×P(B)
=
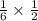
=
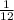
Therefore, probability of rolling a 2 and flipping a head will be