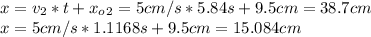Question

At t =0 one toy car is set rolling on a straight track with intial position 17.0 cm , intial velocity -3 cm/s, and constant acceleration 2.30 cm/s^2 . At the same moment , another toy car is set rolling on an adjacent track with initial position 9.5 cm , intial velocity 5.0 cm/s, and constant zero acceleration. (A) at the time, if any, do the two cars have equal speeds? (B) what are their speeds at that time? (c) at what time(s) , if any , do the cars pass each other? (D) what are their location at that time?

Answer 1

a) 5.65 s

b) 5cm/s

c) They will pass each other at both 1.1168 s and 5.84s

d)15.084cm and 38.7 cm

Step-by-step explanation:

For part A, you need to keep in mind that acceleration is the rate of change of velocity per unit of time. For a constant acceleration, this can be told in this way:

`a = (v - v_o)/(t)`

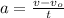
Reordering this equation, we can get v in terms of the initial velocity, the acceleration, and the time elapsed:

`v = at + v_o`

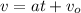
Now, we can get the expressions for velocity of each toy car, and equalize them:

`v_1 =a_1t + v_o_1\\v_2 =a_2t + v_o_2\\v_1 = v2\\a_1t +v_o_1 =a_2t + v_o_2\\(a_1 - a_2)t = v_o_2 - v_o_1\\t = (v_o_2 - v_o_1)/(a_1 - a_2) = (5cm/s - (-3cm/s))/(2.3 cm/s^2 - 0 cm/s^2)= 3.47 s`

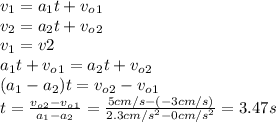
As toy car has no acceleration and, therefore, constant speed, both car will have the same speed when toy car 1 reaches this velocity = 5cm/s

c) The position of car 1, as it follows a constant acceleration motion, is given by this equation:

`x_1 = (1)/(2)a_1t^2 + v_o_1t + x_o_1`

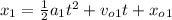
The position for car 2, as it has constant velocity, is given by this equation:

`x_2 = v_2t + x_o_2`

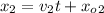
We equalize both equation to find the time where the cars pass each other:

`x_1 = x_2\\(1)/(2)a_1t^2 + v_o_1t + x_o_1 = v_2t+x_o_2\\(1)/(2) a_1t^2 + (v_o_1 - v_2)t + x_o_1 - x_o_2 = 0\\(1)/(2)2.3m/s^2t^2 +(-3cm/s-5cm/s)t+ 17cm - 9.5cm = 0\\1.15t^2 -8t + 7.5 = 0 | a = 1.15, b = -8, c = 7.5\\t = (-b +-√(b^2 - 4ac))/(2a) = 5.84s | 1.1168 s`

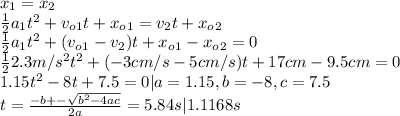
The car will pass each other at both 1.1168s and 5.84s.

For the positions, we solve any of the position equation with the solutions:

`x = v_2*t + x_o_2 = 5cm/s *5.84s + 9.5cm = 38.7 cm\\x = 5cm/s * 1.1168s + 9.5cm = 15.084 cm`