Question

A place-kicker must kick a football from a point 36.0 m (about 40 yards) from the goal. Half the crowd hopes the ball will clear the crossbar, which is 3.05 m high. When kicked, the ball leaves the ground with a speed of 23.6 m/s at an angle of 45.0° to the horizontal. (a) By how much does the ball clear or fall short (vertically) of clearing the crossbar? (Enter a negative answer if it falls short.)

_______m

(b) Does the ball approach the crossbar (and cross above or beneath it) while still rising or while falling?
rising or falling? _________

Answer 1

Part (a) 10.15 m

Part (b) Rising

Step-by-step explanation:

Given,

• Initial speed of the ball = u = 23.6 m/s
• Height of the crossbar = h = 3.05 m
• Distance between the ball and the cross bar = r = 36.0 m
• Angle of projection =
  `\theta\ =\ 45.0^o`
• Initial velocity of the ball in the horizontal direction =
  `u_x\ =\ ucos\theta`

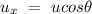
• Initial velocity of the ball in the vertical direction =
  `u_y\ =\ usin\theta`

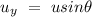
part (a)

Let 't' be the time taken to reach the ball to the cross bar,

In x-direction,

`\therefore r\ =\ u_xt\\\Rightarrow t\ =\ (r)/(u_x)\ =\ (r)/(ucos\theta)\\\Rightarrow t\ =\ (36.0)/(23.6cos45^o)\\\Rightarrow t\ =\ 2.15\ sec`

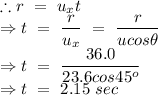
Let y be the height attained by the ball at time t = 2.15 sec,

`y\ =\ u_yt\ \ -\ (1)/(2)gt^2\\\Rightarrow y\ =\ usin\theta t\ -\ (1)/(2)gt^2\\\Rightarrow y\ =\  23.6* sin45^o* 2.15\ -\ 0.5* 9.81\ 2.15^2\\\Rightarrow y\ =\ 13.205\ m`

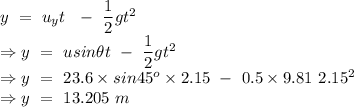
Now Let H be the height by which the ball is clear the crossbar.

`\therefore H\ =\ y\ -\ h\ =\ 13.205\ -\ 3.05\ =\ 10.15\ m`

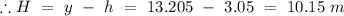
part (b)

At the maximum height the vertical velocity of the ball becomes zero.

i,e,
`v_y\ =\ 0`

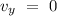
Let h be the maximum height attained by the ball.

`\therefore v_y^2\ =\ u_y^2\ -\ 2gh\\\Rightarrow 0\ =\ (usin\theta)^2\ -\ 2gh\\\Rightarrow h\ =\ ((usin\theta)^2)/(2g)\\\Rightarrow h\ =\ (23.6* sin45.0^o)^2)/(2* 9.81)\\\Rightarrow h\ =\ 14.19\ m`

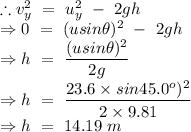
Hence at the cross bar the ball attains the height 13.205 m but the maximum height is 14.19 m. Therefore the ball is rising when it reaches at the crossbar.