Answer:
a) There are 11 balls left in the bag.
b) 4 of the balls in the bag are red.
c) 3 brown, 2 green, 2 white.
d)

e) The probability that the first ball is red and the second is green is:
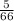
The probability that both balls are red is:
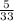
f) The probability that both balls are green is:
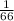
g) The probability that the first ball is brown and the second is white is:
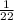
The probability that the first ball is brown and the second is white is:
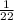
They are the same probabilities.
Explanation:
There are 12 balls in the bag
5 red
3 brown
2 green
2 white
If you draw a red ball and put it aside:
a) How many balls are left in the bag?
There were 12 balls in the bag, and one was put aside.
So, there are 11 balls left in the bag.
b) How many of the balls in the bag are red?
There were 5 red balls in the bag, and one was put aside.
So, there are 4 red balls in the bag.
c) How many are brown? Green? White?
The ball put aside was red, so we still have the same number of the balls of the other colors.
3 brown, 2 green, 2 white.
d) Draw a second ball from the bag. What is the probability that it is green?
There are 11 balls in the bag, 2 of which are green. So the probability that the second ball is green is:

Now put both balls back in the bag and draw two balls without replacing them.
e) What is the probability that the first ball is red and the second ball is green (without replacement)?
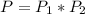
 is the probability that the first ball is red. There are 12 balls, 5 of which are red. So:
is the probability that the first ball is red. There are 12 balls, 5 of which are red. So:
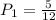
Since there are no replacements, now there are 11 balls in the bag, 2 of which are green. So:
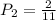
The probability that the first ball is red and the second is green is:
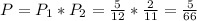
What is the probability that the first ball is red and the second ball is also red (without replacement)?
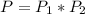
 is the probability that the first ball is red. There are 12 balls, 5 of which are red. So:
is the probability that the first ball is red. There are 12 balls, 5 of which are red. So:
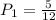
Since there are no replacements, now there are 11 balls in the bag, 4 of which are red. So:
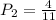
The probability that both balls are red is:
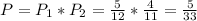
f) What is the probability that the first ball is green and the second ball is also green (without replacement)?
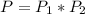
 is the probability that the first ball is green. There are 12 balls, 2 of which are green. So:
is the probability that the first ball is green. There are 12 balls, 2 of which are green. So:
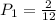
Since there are no replacements, now there are 11 balls in the bag, 1 of which is green. So:
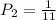
The probability that both balls are green is:
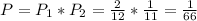
g) What is the probability that the first ball is brown and the second ball is white (without replacement)?
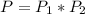
 is the probability that the first ball is brown. There are 12 balls, 3 of which are brown. So:
is the probability that the first ball is brown. There are 12 balls, 3 of which are brown. So:
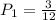
Since there are no replacements, now there are 11 balls in the bag, 2 of which are white. So
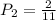
The probability that the first ball is brown and the second is white is:

Would this be different than the probability that the first ball is white and the second ball is brown?
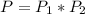
 is the probability that the first ball is white. There are 12 balls, 2 of which are brown. So:
is the probability that the first ball is white. There are 12 balls, 2 of which are brown. So:
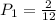
Since there are no replacements, now there are 11 balls in the bag, 3 of which are brown. So
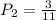
The probability that the first ball is brown and the second is white is:
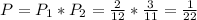
They are the same probabilities.