Question

At some point as you are hiking near a lake, you determine that your campsite is 1.50 km away from you in the direction 30.0° E of N. However, to get back to your campsite, you will need to walk around the lake. You set off due north and walk for 600 m. You then turn in the direction 20.0 W of N and walk an addol1.20 km, before turning and walking directly to your campsite. How far and in what direction was the last leg of your hike?

Answer 1

`r_2 = 976.65 m`

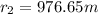
Direction is 19 degree South of East

Step-by-step explanation:

Let say initial position is our reference

so we will have campsite position given as

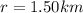`r = 1.50 km` at 20 degree E of N

now we will have

`r = 1500 sin20\hat i + 1500 cos20\hat j`

`r = 513 \hat i + 1409.5\hat j`

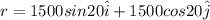
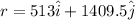
now our displacement to walk around is given as

`d_1 = 600 \hat j`

then we move 20 degree W of N and move 1200 m

so we will have

`d_2 = 1200 sin20(-\hat i) + 1200cos20\hat j`

so our final position is given as

`r_1 = d_1 + d_2`

`r_1 = 600\hat j - 410.4 \hat i + 1127.6\hat j`

`r_1 = -410.4 \hat i + 1727.6\hat j`

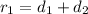
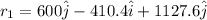
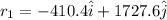
now we know that

`r_1 + r_2 = r`

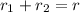
so final leg of the displacement is given as

`r_2 = r - r_1`

`r_2 = (513 \hat i + 1409.5\hat j) - (-410.4 \hat i + 1727.6\hat j)`

`r_2 = 923.4\hat i - 318.1 \hat i`

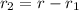
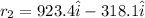
so magnitude is given as

`r_2 = √(923.4^2 + 318.1^2)`

`r_2 = 976.65 m`

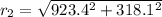
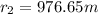
direction is given as

`\theta = tan^(-1)(y)/(x)`

`\theta = tan^(-1)(-318.1)/(923.4)`

`\theta = -19 degree`

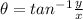
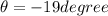
so it is 19 degree South of East