Question

A bird flies 2.0km south and then 1.5km 37° east of south. How far will it have to fly to get back to its original place if it flies in a straight line?

Answer 1

3.324 km

Step-by-step explanation:

d1 = 2 km south

d2 = 1.5 km at 37° east of south

Write the displacements in vector form

`\overrightarrow{d_(1)}=-2\widehat{j}`

`\overrightarrow{d_(2)}=1.5\left (Sin37\widehat{i}-Cos37\widehat{j}  \right )=0.9\widehat{i}-1.2\widehat{j}`

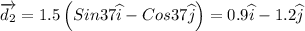
The resultant displacement is given by

`\overrightarrow{d} = \overrightarrow{d_(1)}+ \overrightarrow{d_(2)}`

`\overrightarrow{d} = \left ( 0.9 \right )\widehat{i}+\left ( -2-1.2 \right )\widehat{j}`

`\overrightarrow{d} = \left ( 0.9 \right )\widehat{i}+\left ( -3.2\right )\widehat{j}`

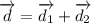
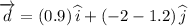
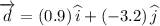
The magnitude of displacement is given by

`d=\sqrt{0.9^(2)+\left ( -3.2 \right )^(2)}=3.324 km`

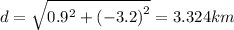
Thus, the bird has to travel 3.324 km in a straight line to return to its original place.