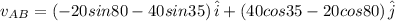Question

Ships A and B leave port together. For the next two hours, ship A travels at 40.0 mph in a direction 35.0° west of north while the ship B travels 80.0° east of north at 20.0 mph . What is the distance between the two ships two hours after they depart? What is the speed of ship A as seen by ship B?

Answer 1

Step-by-step explanation:

Given

Ship A velocity is 40 mph and is traveling 35 west of north

Therefore in 2 hours it will travel
`40* 2=80 miles`

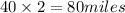
thus its position vector after two hours is

`r_A=-80sin35\hat{i}+80cos35\hat{j}`

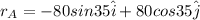
similarly B travels with 20 mph and in 2 hours

`=20* 2=40 miles </p><p>Its position vector[tex]r_B=40sin80\hat{i}+40cos80\hat{j}`

Thus distance between A and B is

`r_(AB)=\left ( -40sin80-80sin35\right )\hat{i}+\left ( 80cos35-40cos80\right )\hat{j}`

`|r_(AB)|=√(\left ( -40sin80-80sin35\right )^2+\left ( 80cos35-40cos80\right )^2)`

`|r_(AB)|=103.45 miles`

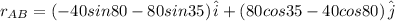
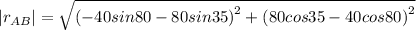
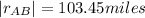
Velocity of A

`v_A=-40sin35\hat{i}+40cos35\hat{j}`

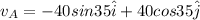
Velocity of B

`v_B=20sin80\hat{i}+20cos80\hat{j}`

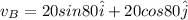
Velocity of A w.r.t B

`v_(AB)=v_A-v_B`

`v_(AB)=\left ( -20sin80-40sin35\right )\hat{i}+\left ( 40cos35-20cos80\right )\hat{j}`