Answer:
t = 71.47 min
Step-by-step explanation:
Using integrated rate law for first order kinetics as:
![[A_t]=[A_0]e^(-kt)](https://img.qammunity.org/2020/formulas/chemistry/college/wgh5hifj7f12vitsa51kophgqrxxcfit2c.png)
Where,
![[A_t]](https://img.qammunity.org/2020/formulas/chemistry/college/wbj92t0z4axifcyqa24z3ary269op2iva8.png) is the concentration at time t
is the concentration at time t
![[A_0]](https://img.qammunity.org/2020/formulas/chemistry/college/izynxfnwyud2ghdog9l8ny0mhzwshbud6r.png) is the initial concentration
is the initial concentration
Given:
20.8 % is decomposed which means that 0.208 of
![[A_0]](https://img.qammunity.org/2020/formulas/chemistry/college/izynxfnwyud2ghdog9l8ny0mhzwshbud6r.png) is decomposed. So,
is decomposed. So,
![\frac {[A_t]}{[A_0]}](https://img.qammunity.org/2020/formulas/chemistry/college/rdky51ah6e4fo6vkh0t5pkijdlldqfq8xn.png) = 1 - 0.208 = 0.792
= 1 - 0.208 = 0.792
t = 7.8 min
![\frac {[A_t]}{[A_0]}=e^(-k* t)](https://img.qammunity.org/2020/formulas/chemistry/college/tixyocmkbxlfsradct604h51a1nrscvy5b.png)

k = 0.0299 min⁻¹
Also,
Given:
88.2 % is decomposed which means that 0.882 of
![[A_0]](https://img.qammunity.org/2020/formulas/chemistry/college/izynxfnwyud2ghdog9l8ny0mhzwshbud6r.png) is decomposed. So,
is decomposed. So,
![\frac {[A_t]}{[A_0]}](https://img.qammunity.org/2020/formulas/chemistry/college/rdky51ah6e4fo6vkh0t5pkijdlldqfq8xn.png) = 1 - 0.882 = 0.118
= 1 - 0.882 = 0.118
t = ?
![\frac {[A_t]}{[A_0]}=e^(-k* t)](https://img.qammunity.org/2020/formulas/chemistry/college/tixyocmkbxlfsradct604h51a1nrscvy5b.png)
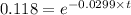
t = 71.47 min