Question

A researcher wants to provide a rabbit exactly 162 units of​protein, 72 units of​ carbohydrates, and 30 units of vitamin A. The rabbit is fed three types of food. Each gram of Food A has 5 units of​ protein, 2 units of​ carbohydrates, and 1unit of vitamin A. Each gram of Food B contains 11 units of​ protein, 5 units of​carbohydrates, and 2 units of vitamin A. Each gram of Food C contains 23 units of​ protein, 11 units of​ carbohydrates, and 4 units of vitamin A. How many grams of each food should the rabbit be​ fed?

Answer 1

The rabbit should be fed:

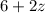`6 + 2z` grams of food A

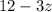`12 - 3z` grams of food B

`z` grams of food C

For
`z \leq 4`.

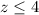Explanation:

This can be solved by a system of equations.

I am going to say that x is the number of grams of food A, y is the number of grams of food B and z is the number of grams of Food C.

The problem states that:

A researcher wants to provide a rabbit exactly 162 units of ​protein:

There are 5 units of protein in each gram of food A, 11 units of protein in each gram of food B and 23 units of protenin in each gram of food C. So

`5x + 11y + 23z = 162`

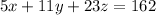
A researcher wants to provide a rabbit exactly 72 units of carbohydrates:

There are 2 units of carbohydrates in each gram of food A, 5 units of carbohydrates in each gram of food B and 11 units of carbohydrates in each gram of food C. So:

`2x + 5y + 11z = 72`

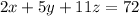
A researcher wants to provide a rabbit exactly 30 units of Vitamin A:

There is 1 unit of Vitamin A in each gram of food A, 2 units of Vitamin A in each gram of food B and 4 units of Vitamin A in each gram of food C. So:

`x + 2y + 4z = 30`.

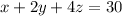We have to solve the following system of equations:

`5x + 11y + 23z = 162`

`2x + 5y + 11z = 72`

`x + 2y + 4z = 30`.

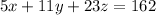
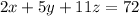
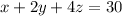I think that the easier way to solve this is reducing the augmented matrix of this system.

This system has the following augmented matrix:

`\left[\begin{array}{cccc}5&11&23&162\\2&5&11&72\\1&2&4&30\end{array}\right]`

To help reduce this matrix, i am going to swap the first line with the third

`L_(1) <-> L_(3)`

Now we have the following matrix:

`\left[\begin{array}{cccc}1&2&4&30\\2&5&11&72\\5&11&23&162\end{array}\right]`

Now i am going to do these following operations, to reduce the first row:

`L_(2) = L_(2) - 2L_(1)`

`L_(3) = L_(3) - 5L_(1)`

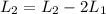
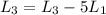
Now we have

`\left[\begin{array}{cccc}1&2&4&30\\0&1&3&12\\0&1&3&12\end{array}\right]`

Now, to reduce the second row, i do:

`L_(3) = L_(3) - L_(2)`

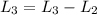
The matrix is:

`\left[\begin{array}{cccc}1&2&4&30\\0&1&3&12\\0&0&0&0\end{array}\right]`

This means that z is a free variable, so we are going to write y and x as functions of z.

From the second line, we have

`y + 3z = 12`

`y = 12 - 3z`

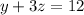
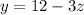
From the first line, we have

`x + 2y + 4z = 30`

`x + 2(12 - 3z) + 4z = 30`

`x + 24 - 6z + 4z = 30`

`x = 6 + 2z`

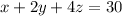
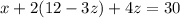
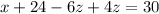
Our solution is:
`x = 6 + 2z, y = 12 - 3z, z = z`.

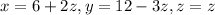However, we can not give a negative number of grams of a food. So

`y \geq 0`

`12 - 3z \geq 0`

`-3z \geq -12 *(-1)`

`3z \leq 12`

`z \leq 4`

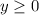
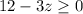
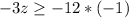
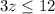
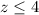
The rabbit should be fed:

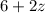`6 + 2z` grams of food A

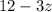`12 - 3z` grams of food B

`z` grams of food C

For
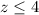`z \leq 4`.