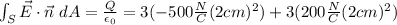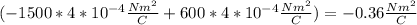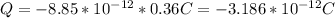Question

Three faces of a cube of side length 2 cm each have a uniform electric field of magnitude 500 N/C pointing directly inward. The other three faces each have a uniform electric field of magnitude 200 N/C pointing directly outward. What is the magnitude and sign of the net charge enclosed in the cube?

Answer 1

`Q=-8.85*10^(-12)*0.36 C =-3.186*10^(-12) C`

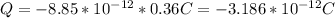
(negative charge)

Step-by-step explanation:

Hi!

To solve this problem we use Gauss Law for electric fields, which relates the flux of electric field E through a closed surface S with the charge Q enclosed by that surface:

`\int_(S) \vec{E}\cdot \vec{n} \;dA = (Q)/(\epsilon_0)`

`\vec{n} = \text{outwards surface normal}\\\epsilon_0 = 8.85*10^(-12)(C^2)/(Nm^2)`

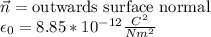
In this problem S is a cube of side length 2cm. The integral is easy because the electric field is uniform in each face, and normal to the face. The total integral is the sum of the integrals in each of the six faces.

`\int_(S) \vec{E}\cdot \vec{n} \;dA = (Q)/(\epsilon_0) = 3(-500(N)/(C) (2cm)^2) + 3(200(N)/(C) (2cm)^2)`

`(-1500*4*10^(-4)(Nm^2)/(C) + 600*4*10^(-4)(Nm^2)/(C) )=-0.36(Nm^2)/(C)`

`Q=-8.85*10^(-12)*0.36 C =-3.186*10^(-12) C`