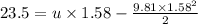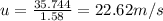Question

Alex climbs to the top of a tall tree while his friend Gary waits on the ground below. Alex throws down a ball at 8 m/s from 50 m above the ground at the same time Gary throws a ball up. At what speed must Gary throw a ball up in order for the two balls to cross paths 25 m above the ground? The starting height of the ball thrown upward is 1.5 m above the ground. Ignore the effects of air resistance. whats the answer in m/s?

Answer 1

Answer:22.62 m/s

Step-by-step explanation:

Given

two balls are separated by a distance of 50 m

Alex throws the ball from a height of 50 m with a velocity of 8 m/s and Gary launches a ball with some velocity exactly at the same time.

ball from ground travels a distance of 25 m in t sec

For Person on tree

`25=ut+(1)/(2)gt^2`

`25=8t+(1)/(2)* 9.81* t^2--------1`

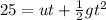
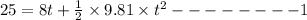
For person at ground

`23.5=ut-(1)/(2)gt^2---------2`

Solve equation (1)

`50=16t+9.81t^2`

`9.81t^2+16t-50=0`

`t=(-16\pm√(256+4* 50* 9.81))/(2* 9.81)=(47.1-16)/(19.62)=1.58 s`

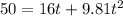
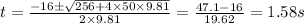
put the value of t in equation 2

`23.5=u* 1.58-(9.81* 1.58^2)/(2)`

`u=(35.744)/(1.58)=22.62 m/s`