Answer:
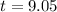 weeks
weeks
Explanation:
The mass of this particular substance can be modeled by the following exponential function:

In which
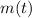 is the mass in function of time,
is the mass in function of time,
 is the initial mass and r, in decimal, is the growth rate of the mass.
is the initial mass and r, in decimal, is the growth rate of the mass.
The problem states that:
The mass of a particular substance is known to grow exponentially at a rate of 17% per week. Its initial mass was 12 grams and, after t weeks, it weighed 56 grams. So:


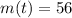
We have to solve this equation for t. So:

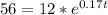
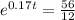
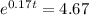
To solve for
 , we put ln in both sides
, we put ln in both sides
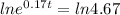
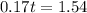
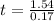
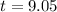 weeks
weeks