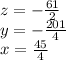Answer:
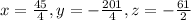
Explanation:
We start by putting our equation in a matricial form:
![\left[\begin{array}{cccc}12&2&1&4\\3&3&-4&5\\2&-2&4&1\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/tyl9sir9ry4se1opyimwt9dfdzybkbdpyq.png)
Then, we multiply the second row by 4 and substract the first row:
![\left[\begin{array}{cccc}12&2&1&4\\0&10&-17&16\\2&-2&4&1\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/cc4898z3pp0wlwj4xroi661f36exq8hntm.png)
Now, multiply the third row by 6 and substract the first row:
![\left[\begin{array}{cccc}12&2&1&4\\0&10&-17&16\\0&-14&23&2\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/9lkzjjx6twb3sboipfi0pcgzpzt4b2blcl.png)
Next, we will add
 times the second row to the third row:
times the second row to the third row:
![\left[\begin{array}{cccc}12&2&1&4\\0&10&-17&16\\0&0&(-4)/(5)&(122)/(5)\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/9c0soadrfkqqa8zvp9q9owaj395ddu3b9f.png)
Now we can solve
 to obtain
to obtain
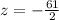
Then
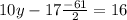 wich implies that
wich implies that

Finally
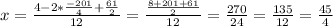 .
.