Answer:
a)
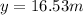
b)
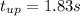
c)
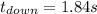
d)
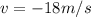
Step-by-step explanation:
a) To find the highest point of the ball we need to know that at that point the ball stops going up and its velocity become 0
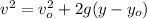
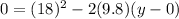
Solving for y
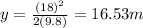
b) To find how long does it take to reach that point:

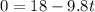
Solving for t
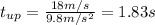
c) To find how long does it take to hit the ground after it reaches its highest point we need to find how long does it take to do the whole motion and then subtract the time that takes to go up

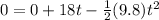
Solving for t
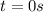 or
or

Since time can not be negative, we choose the second option
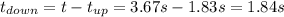
d) To find the velocity when it returns to the level from which it started we need to use the following formula:


The sign means the ball is going down