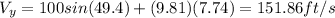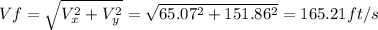Question

A projectile is fired with initial speedv -100 feet per second from a height of h 0 feet atan angle of θ-7/6 above the horizontal. Assuming that the only force acting on the object is gravity, find the maximum altitude, horizontal range and speed at impact.

Answer 1

Maximum altitude: 497.96 ft

Horizontal range: 1007.37 ft

Speed at impact: 165.21 ft/s

Step-by-step explanation:

angle(α) = atan (7/6) = 49.4°

Maximum altitude is given by the formula:

`h=(V_0^2sin^2\alpha )/(2g)`

`h=(100^2 sin^2(49.4))/(2*9.81) =(9770)/(19.62)=497.96 ft/s`

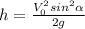
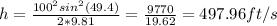
Horizontal range is given by the formula:

`X=(V_0^2sin(2\alpha))/(g)`

`X=(100^2sin(2*49.4))/(*9.81)=1007.37 ft`

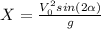
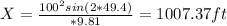
Speed at impact is given by the formula:

`V_f=√(V_x^2 + Vy^2)`

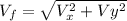
where:

`V_x= V_0cos(\alpha )= 100cos(49.4)=65.07 ft/s`

`V_y=V_0sin(\alpha ) + gt=100sin(49.4)+9.81(t)`

`t=(V_0sin(\alpha) )/(g)=(100sin(49.4))/(9.81)=7.74s`

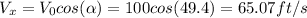
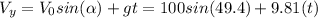
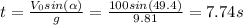
So;

`V_y= 100sin(49.4)+(9.81)(7.74)= 151.86 ft/s`

`Vf=√(V_x^2 + V_y^2) =√(65.07^2+151.86^2)=165.21 ft/s`