Question

The cheetah is considered the fastest running animal in the world. Cheetahs can accelerate to a speed of 21.7 m/s in 2.50 s and can continue to accelerate to reach a top speed of 28.7 m/s. Assume the acceleration is constant until the top speed is reached and is zero thereafter. 1) Express the cheetah's top speed in mi/h. (Express your answer to three significant figures.) 2) Starting from a crouched position, how long does it take a cheetah to reach its top speed? (Express your answer to three significant figures.) 3) How far does it travel in that time? (Express your answer to three significant figures.) 4) If a cheetah sees a rabbit 120 m away, how long will it take to reach the rabbit, assuming the rabbit does not move?(Express your answer to three significant figures.)

Answer 1

The cheetah's top speed of 28.7 m/s is approximately 64.2 mi/h. It takes a cheetah 3.31 seconds to reach its top speed, traveling a distance of 47.4 meters during this acceleration. To reach a stationary rabbit 120 meters away, it would take the cheetah a total of 5.84 seconds.

Step-by-step explanation:

The question involves converting speeds from meters per second to miles per hour, finding the time taken to achieve a certain speed, calculating the distance traveled in that time, and determining the time required to reach a target.

1. To convert the cheetah's top speed from meters per second (m/s) to miles per hour (mi/h), we use the conversion factor of 1 m/s = 2.23694 mi/h. The top speed of 28.7 m/s is equivalent to 64.2 mi/h to three significant figures.
2. The time taken to reach the top speed can be found using the acceleration formula: a = (v - u) / t, where 'v' is final velocity, 'u' is initial velocity, and 't' is time. Since the cheetah starts from rest (u = 0), we know it reaches a speed of 21.7 m/s in 2.5 s, implying an acceleration of 21.7 m/s / 2.5 s = 8.68 m/s². To then reach the top speed of 28.7 m/s, the time t = (28.7 m/s) / (8.68 m/s²), which is approximately 3.31 s.
3. The distance traveled while accelerating can be found using the kinematic equation: d = ut + (1/2)at². As the cheetah starts from rest (u = 0), the distance is d = (1/2)(8.68 m/s²)(3.31 s)², which equals 47.4 m.
4. If the cheetah sees a rabbit 120 m away and accelerates towards it, we need to find the time taken to cover this distance. The cheetah covers 47.4 m while reaching top speed, which takes 3.31 s. The remaining distance at top speed is 120 m - 47.4 m = 72.6 m. The time taken to cover this at 28.7 m/s is 72.6 m / 28.7 m/s = 2.53 s. The total time to reach the rabbit is 3.31 s + 2.53 s = 5.84 s.

Answer 2

1) 64.2 mi/h

2) 3.31 seconds

3) 47.5 m

4) 5.26 seconds

Step-by-step explanation:

t = Time taken = 2.5 s

u = Initial velocity = 0 m/s

v = Final velocity = 21.7 m/s

s = Displacement

a = Acceleration

1) Top speed = 28.7 m/s

1 mile = 1609.344 m

`1\ m=(1)/(1609.344)\ miles`

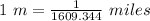
1 hour = 60×60 seconds

`1\ s=(1)/(3600)\ hours`

`28.7\ m/s=((28.7)/(1609.344))/((1)/(3600))=64.2\ mi/h`

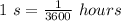
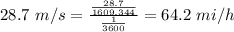
Top speed of the cheetah is 64.2 mi/h

Equation of motion

`v=u+at\\\Rightarrow a=(v-u)/(t)\\\Rightarrow t=(21.7-0)/(2.5)\\\Rightarrow a=8.68\ m/s^2`

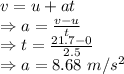
Acceleration of the cheetah is 8.68 m/s²

2)

`v=u+at\\\Rightarrow t=(v-u)/(a)\\\Rightarrow t=(28.7-0)/(8.68)\\\Rightarrow t=3.31\ s`

It takes a cheetah 3.31 seconds to reach its top speed.

3)

`v^2-u^2=2as\\\Rightarrow s=(v^2-u^2)/(2a)\\\Rightarrow s=(28.7^2-0^2)/(2* 8.68)\\\Rightarrow s=47.5\ m`

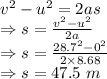
It travels 47.5 m in that time

4) When s = 120 m

`s=ut+(1)/(2)at^2\\\Rightarrow 120=0* t+(1)/(2)* 8.68* t^2\\\Rightarrow t=\sqrt{(120* 2)/(8.68)}\\\Rightarrow t=5.26\ s`

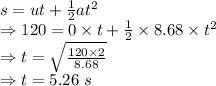
The time it takes the cheetah to reach a rabbit is 120 m is 5.26 seconds