Question

Suppose you invest $750.00 in a fund earning 6% simple discount. A certain time later you withdraw the investment (principal and interest) and invest it in another fund earning 3.5% compound interest for two years. How much total time (INCLUDING THE TWO YEARS earning compound interest) will be required for the original $750.00 to accumulate to $1,000.00? (two decimal places)

Answer 1

4.08 + 2 = 6.08 years

Explanation:

we know that

Simple Interest(S.I.) = (P × R × T) ÷ 100

where, P = Principal = 750

R = Rate = 6%

T = unknown

⇒ S.I. = (750 × 6 × t)÷ 100

⇒ S.I. = 45t

Also, Amount = S.I + Principal

⇒ Amount = 750 + 45t

Now Formula for Compound Interest is:

`A = P(1+(r)/(100))^(t)`

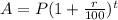
where A = Amount

=1000

P = Principle

r = rate

t = total number of year

Here, P = 750 + 45t, r = 3.5% , and t = 2.

Putting all these values in above formula:

`1000 = (750 + 45t)(1+(3.5)/(100))^(2)`

⇒
`1000 = (750 + 45t)(1.071)`

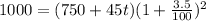
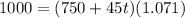
⇒ t = 4.08

Hence, total time required will be 2 + 4.08 = 6.08 years.