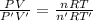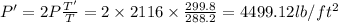Question

A tank of volume 0.25 ft is designed to contain 50 standard cubic feet of air. The temperature is 80° F.Calculate the pressure inside the tank. One standard cubic foot of air occupies foot at standard 'temperature and pressure (T 59° F and p= 2116 lb/ft2). one cubic

Answer 1

The inside Pressure of the tank is
`4499.12 lb/ft^(2)`

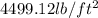
Solution:

As per the question:

Volume of tank,
`V = 0.25 ft^(3)`

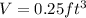
The capacity of tank,
`V' = 50ft^(3)`

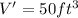
Temperature, T' =
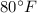`80^(\circ)F` = 299.8 K

Temperature, T =
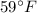`59^(\circ)F` = 288.2 K

Now, from the eqn:

PV = nRT (1)

Volume of the gas in the container is constant.

V = V'

Similarly,

P'V' = n'RT' (2)

Also,

The amount of gas is double of the first case in the cylinder then:

n' = 2n

`\]frac{n'}{n} = 2`

where

n and n' are the no. of moles

Now, from eqn (1) and (2):

`(PV)/(P'V') = (nRT)/(n'RT')`

`P' = 2P(T')/(T) = 2* 2116* (299.8)/(288.2) = 4499.12 lb/ft^(2)`