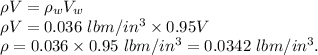Question

According to Archimedes' principle, the mass of a floating object equals the mass of the fluid displaced by the object. A 150-lbm swimmer is floating in a nearby pool; 95% of his or her body's volume is in the water while 5% of his or her body's volume is above water. Determine the density of the swimmer's body. The density of water is 0.036lbm/in^3.

Answer 1

Density of the swimmer =
`0.0342\ lbm/in^3`.

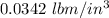Step-by-step explanation:

Assuming,

• 
  `\rho` = density of the swimmer.

• 
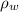  `\rho_w` = density of the water.

• 
  `m` = mass of the swimmer.

• 
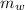  `m_w` = mass of the water displaced by the swimmer.

• 
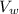  `V_w` = volume of the displaced water.

• 
  `V` = volume of the swimmer.

Given:

• 
  `m=150\ lbm.`
• 
  `\rho_w = 0.036\ lbm/in^3.`

The density of an object is defined as the mass of the object per unit volume.

Therefore,

`\rho =(m)/(V)\ \Rightarrow m = \rho V\ \ .........\ (1).`

Since only 95% of the body of the swimmer is inside the water, therefore,

`V_w = 95\%\ \text{of}\ V=(95)/(100)* V = 0.95V.`

According to Archimedes' principle,

`m=m_w\\`

Using (1),

`\rho V=\rho_w V_w\\\rho V = 0.036\ lbm/in^3* 0.95 V\\\rho=0.036* 0.95\ lbm/in^3=0.0342\ lbm/in^3.`