Question

You drop a rock into a deep well and hear the sounds of it hitting the bottom 5.50 s later. If the speed of sound is 340 m/s, determine the depth of the well.

Answer 1

The depth of well equals 120.47 meters.

Step-by-step explanation:

The time it takes the sound to reach our ears is the sum of:

1) Time taken by the rock to reach the well floor.

2) Time taken by the sound to reach our ears.

The Time taken by the rock to reach the well floor can be calculated using second equation of kinematics as:

`h=ut+(1)/(2)gt^2`

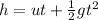
where,

'u' is initial velocity

't' is the time to cover a distance 'h' which in our case shall be the depth of well.

'g' is acceleration due to gravity

Since the rock is dropped from rest hence we infer that the initial velocity of the rock =0 m/s.

Thus the time to reach the well base equals

`h=(1)/(2)gt_1^2\\\\\therefore t_(1)=\sqrt(2h)/(g)`

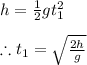
Since the propagation of the sound back to our ears takes place at constant speed hence the time taken in the part 2 is calculated as

`t_(2)=(h)/(Speed)=(h)/(340)`

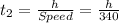
Now since it is given that

`t_(1)+t_(2)=5.50`

Upon solving we get

`\sqrt{(2h)/(g)}+(h)/(340)=5.5\\\\\sqrt{(2h)/(g)}=5.5-(h)/(340)\\\\(\sqrt{(2h)/(g)})^(2)=(5.5-(h)/(340))^(2)\\\\(2h)/(g)=5.5^2+(h^2)/((340^2))-2* 5.5* (h)/(340)`

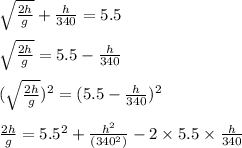
Solving the quadratic equation for 'h' we get

h = 120.47 meters.