Question

A. How many atoms of helium gas fill a spherical balloon of diameter 29.6 cm at 19.0°C and 1.00 atm? b. What is the average kinetic energy of the helium atoms?

c. What is the rms speed of the helium atoms?

Answer 1

a) 3.39 × 10²³ atoms

b) 6.04 × 10⁻²¹ J

c) 1349.35 m/s

Step-by-step explanation:

Given:

Diameter of the balloon, d = 29.6 cm = 0.296 m

Temperature, T = 19.0° C = 19 + 273 = 292 K

Pressure, P = 1.00 atm = 1.013 × 10⁵ Pa

Volume of the balloon =
`(4)/(3)\pi((d)/(2))^3`

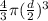
or

Volume of the balloon =
`(4)/(3)\pi((0.296)/(2))^3`

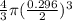
or

Volume of the balloon, V = 0.0135 m³

Now,

From the relation,

PV = nRT

where,

n is the number of moles

R is the ideal gas constant = 8.314 kg⋅m²/s²⋅K⋅mol

on substituting the respective values, we get

1.013 × 10⁵ × 0.0135 = n × 8.314 × 292

or

n = 0.563

1 mol = 6.022 × 10²³ atoms

Thus,

0.563 moles will have = 0.563 × 6.022 × 10²³ atoms = 3.39 × 10²³ atoms

b) Average kinetic energy =
`(3)/(2)* K_BT`

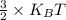
where,

Boltzmann constant,
`K_B=1.3807*10^(-23)J/K`

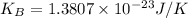
Average kinetic energy =
`(3)/(2)*1.3807*10^(-23)*292`

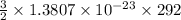
or

Average kinetic energy = 6.04 × 10⁻²¹ J

c) rms speed =
`(3RT)/(m)`

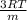
where, m is the molar mass of the Helium = 0.004 Kg

or

rms speed =
`(3*8.314*292)/(0.004)`

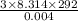
or

rms speed = 1349.35 m/s