Question

Red and blue light enter together into a glass plate of 10 cm. What is the distance between red and blue light whenthe light emerges from the plate. n(blue) = 1.6, n(red) = 1.3

Answer 1

The distance between the emergent red and blue light is 3 cm

Solution:

As per the question:

Thickness of the glass plate, s = 10 cm = 0.1 m

Refractive index of blue light,
`n_(blue) = 1.6`

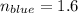
Refractive index of blue light,
`n_(red) = 1.3`

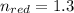
Now, to calculate the distance between red and blue light as it emerges from the plate:

We know that refractive index is given as the ratio of speed of light in vacuum, c or air to that in medium,
`v_(m)`.

`n = (c)/(v_(m))`

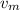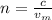
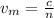`v_(m) = (c)/(n)` (1)

Since, c is constant, thus

n ∝
`(1)/(v_(m))`

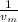
Now, the refractive index of blue light is more than that of red light thus its speed in medium is lesser than red light.

Now, time taken, t by red and blue light to emerge out of the glass slab:

`s = v_(m)* t`

`t = (s)/(v_(blue)) = (sn_(blue))/(c)`

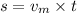
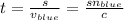
In the same time, red light also traveled through the glass covering some distance in air say x

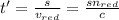`t' = (s)/(v_(red)) = (sn_(red))/(c)` (2)

Time taken by red light to cover 'x' distance in vacuum is t'':

`t`

Now,

t = t' + t" (3)

From eqn (1), (2) and (3):

`(sn_(blue))/(c) = (sn_(red))/(c) + (x)/(c)`

Now, putting appropriate values in the above eqn:

`(0.1* 1.6)/(c) = (0.1* 1.3)/(c) + (x)/(c)`

`(0.16)/(c) - (0.13)/(c) = (x)/(c)`

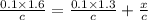
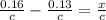
x = 0.03 m = 3 cm

Answer 2

The shift in the color's depends on the angle of incidence, for a special case when the angle of incidence is along the normal to the surface no shift will be observed.

Step-by-step explanation:

When a ray of light is incident on a medium perpendicular to it it does not undergo any refraction thus no shift will be seen.