Question

You want to prepare 500.0 mL of 1.000 M KNO3 at 20°C, but the lab (and water) temperature is 24°C at the time of preparation. How many grams of solid KNO3 (density = 2.109 g/mL) should be dissolved in a volume of 500.0 mL at 24°C to give a concentration of 1.000 M at 20°C? What apparent mass of KNO; weighed in air is required?

Answer 1

Step-by-step explanation:

As per the given data, at a higher temperature, at
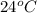`24^(o)C`, the solution will occupy a larger volume than at
`20^(o)C`.

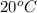Since, density is mass divided by volume and it will decrease at higher temperature.

Also, concentration is number of moles divided by volume and it decreases at higher temperature.

At
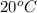`20^(o)C`, density of water=0.9982071 g/ml

Therefore,
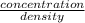`(concentration)/(density)` will be calculated as follows.

=
`(C_(1))/(d_(1))`

=
`(1.000 mol/L)/(0.9982071 g/ml)`

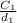
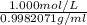
= 1.0017961 mol/g

At
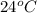`24^(o)C`, density of water = 0.9972995 g/ml

Since,
`(concentration)/(density)` =
`(C_(2))/(d_(2))`

=
`(C_(2))/(0.9972995)`

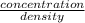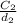
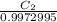
Also,
`(C_(1))/(d_(1))` =
`(C_(2))/(d_(2))`

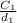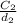
so, 1.0017961 mol/g =
`(C_(2))/(0.9972995)`

`C_(2) = 1.0017961 * 0.9972995`

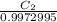
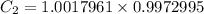
= 0.9990907 mol/L

Therefore, in 500 ml, concentration of
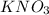`KNO_(3)` present is calculated as follows.

`C_(2)` =
`(concentration)/(volume)`

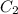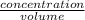
0.9990907 mol/L =
`(concentration)/(0.5 L)`

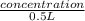
concentration = 0.49954537 mol

Hence, mass (m'') =
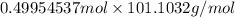`0.49954537 mol * 101.1032 g/mol` = 50.5056 g (as molar mass of
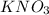`KNO_(3)` = 101.1032 g/mol).

Any object displaces air, so the apparent mass is somewhat reduced, which requires buoyancy correction.

Hence, using Buoyancy correction as follows,

m =
`m''' * ((1 - (d_(air))/(d_(weights))))/((1 - (d_(air))/(d)))}`

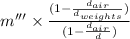
where,
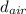`d_(air)` = density of air = 0.0012 g/ml

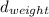`d_(weight)` = density of callibration weights = 8.0g/ml

d = density of weighed object

Hence, the true mass will be calculated as follows.

True mass(m) =
`50.5056 * ((1 - (0.0012)/(8.0)))/((1 - ((0.0012)/(2.109)))`

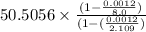
true mass(m) = 50.5268 g

= 50.53 g (approx)

Thus, we can conclude that 50.53 g apparent mass of
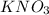`KNO_(3)` needs to be measured.