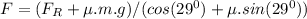Question

Newton's second law: Rudolph the red nosed reindeer is pulling a 25 kg sled across the snow in a field. The coefficient of kinetic friction is .12 The rope that is pulling the sled is coming off at a 29 degree angle above the horizontal. Find the force in the rope when the acceleration is .12 m/s^2.

Answer 1

`F=39,68N`

Step-by-step explanation:

Data:

Mass
`m=25 Kg`

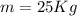
Coefficient of kinetic friction
`\mu=0.12`

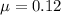
Angle =
`29^(0)`

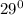
Acceleration =
`0.12 (m)/(s^(2) )`

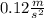
Solution:

By Newton's first law we know that for the x-axis:

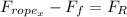`F_(rope_x)-F_f=F_R` Where
`F_R` is the resulting force, and
`F_f` is the friction force.

And for the y-axis:

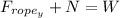`F_(rope_y)+N=W`, where N is the normal force, and W is the weight of the sled.

We know that the resulting force's acceleration is
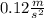`0.12 (m)/(s^(2) )`, and by using Newton's second law, we obtain:

`F=m.a`

`F_R=25Kg. 0.12(m)/(s^2) \\ F_R=3N` .

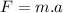
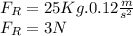Now, the horizontal component of the force in the rope will be given by

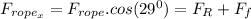`F_(rope_x)=F_(rope).cos(29^0)=F_R+F_f`, since the resulting force is completely on the x-axis, and the friction opposes to the speed of the sled.

To obtain the friction force, we must know the normal force:

`F_f=\mu. N`

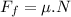
Clearing N in the y-axis equation:

`N=W-F_(rope_y)=W-F_(rope).sin(29^0)`

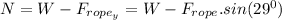
So we can express the x-axis equation as follows:

`F.cos(29^0)=F_R+\mu.(W-F_(rope).sin(29^0))`

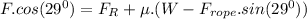
Finally, solving for F we get

`F = (F_R + \mu. m.g) / (cos (29^0) + \mu.sin (29^0))`

`F=39,68N`