Answer:
(a) angles of maxima = 13.9°, 28.7° , 46°, 73.7° on either side
b] largest order = 4
Step-by-step explanation:
(a) for diffraction maxima,

Here, m is the order,
 is the wavelength,
is the wavelength,
 is the angle at which maxima occur, d is inter planar spacing.
is the angle at which maxima occur, d is inter planar spacing.
And we know that lines per mm (N) is related with d as,

Given that the wavelength is,

And
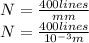
Now,
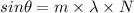
Therefore,
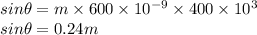
Here, m can be 1,2,3,4 as sin theta has to be less than 1.

Therefore, angles of maxima = 13.9°, 28.7° , 46°, 73.7° on either side
b] largest order = 4