Answer:
Approximately 18 units will be produced before the output rate exceeds 12 units per hour.
Step-by-step explanation:
The learning curve formula is given by:
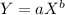
In which:
Y is the average time per unit.
X is the cumulative number of units produced.
a is the time required to produe the first unit
b = log of learning rate/log 2
In our problem, we have:
Y = 12 units per hour. We are working in minutes, what is the average time per unit?
60 minutes - 12 units
Y minutes - 1 unit
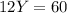

So Y = 5.
X is the value we want to find
a = 30
b =
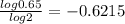
So
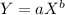
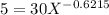
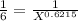
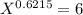
![\sqrt[0.6215]{X^(0.6215)} = \sqrt[0.6215]{6}](https://img.qammunity.org/2020/formulas/mathematics/college/hfa1xpf3sqkr5p73gr6uwe3y1udr7ld8xg.png)
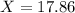
Approximately 18 units will be produced before the output rate exceeds 12 units per hour.