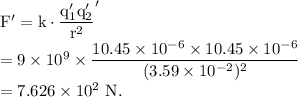Answer:
(a):

(b):
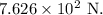
Step-by-step explanation:
Given:
- Charge on one sphere,
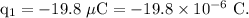
- Charge on second sphere,
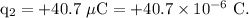
- Separation between the spheres,
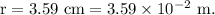
Part (a):
According to Coulomb's law, the magnitude of the electrostatic force of interaction between two static point charges is given by
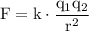
where,
k is called the Coulomb's constant, whose value is
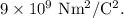
From Newton's third law of motion, both the spheres experience same force.
Therefore, the magnitude of the force that each sphere experiences is given by

The negative sign shows that the force is attractive in nature.
Part (b):
The spheres are identical in size. When the spheres are brought in contact with each other then the charge on both the spheres redistributes in such a way that the net charge on both the spheres distributed equally on both.
Total charge on both the spheres,
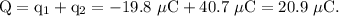
The new charges on both the spheres are equal and given by
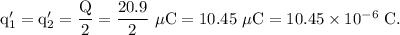
The magnitude of the force that each sphere now experiences is given by