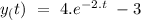Question

Find a formula for Y(t) with Y(0)=1 and draw its graph. What is Y\infty?

a. Y'+2Y=6

b. Y'+2Y=-6

Answer 1

`(a)\ y(t)\ =\ -2e^(-2t)+3`

`(b)\ y(t)\ =\ 4e^(-2t)-3`

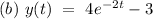
Explanation:

(a) Given differential equation is

Y'+2Y=6

=>(D+2)y = 6

To find the complementary function, we will write

D+2=0

=> D = -2

So, the complementary function can be given by

`y_c(t)\ =\ C.e^(-2t)`

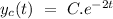
To find the particular integral, we will write

`y_p(t)\ =\ (6)/(D+2)`

`=\ (6.e^(0.t))/(D+2)`

`=\ (6)/(0+2)`

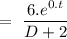
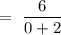
= 3

so, the total solution can be given by

`y_(t)\ =\ C.F+P.I`

`=\ C.e^(-2t)\ +\ 3`

`y_(0)=C.e^(-2.0)\ +\ 3`

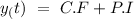
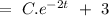
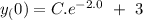
but according to question

1 = C +3

=> C = -2

So, the complete solution can be given by

`y_(t)\ =\ -2.e^(-2.t)\ +\ 3`

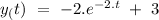
(b) Given differential equation is

Y'+2Y=-6

=>(D+2)y = -6

To find the complementary function, we will write

D+2=0

=> D = -2

So, the complementary function can be given by

`y_c(t)\ =\ C.e^(-2t)`

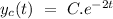
To find the particular integral, we will write

`y_p(t)\ =\ (-6)/(D+2)`

`=\ (-6.e^(0.t))/(D+2)`

`=\ (-6)/(0+2)`

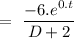
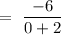
= -3

so, the total solution can be given by

`y_(t)\ =\ C.F+P.I`

`=\ C.e^(-2t)\ -\ 3`

`y_(0)\ =C.e^(-2.0)\ -\ 3`

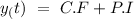
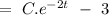
but according to question

1 = C -3

=> C = 4

So, the complete solution can be given by

`y_(t)\ =\ 4.e^(-2.t)\ -3`