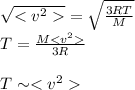Question

For a monatomic ideal gas, temperature is proportional to : the square of the average atomic velocity.

the average atomic velocity.
the atomic mean free path.
the number of atoms.

Answer 1

The temperature of a monatomic ideal gas is directly proportional to the average atomic velocity.

Step-by-step explanation:

The temperature of a monatomic ideal gas is directly proportional to the average atomic velocity. As the temperature increases, the average atomic velocity also increases. This relationship is a result of the fact that temperature is a measure of the kinetic energy of the gas particles, and the average velocity is related to the kinetic energy. Therefore, temperature and average atomic velocity are directly proportional in a monatomic ideal gas.

Answer 2

the square of the average atomic velocity.

Step-by-step explanation:

From the formulas for kinetic energy and temperature for a monoatomic gas, which has three translational degrees of freedom, the relationship between root mean square velocity and temperature is as follows:

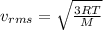`v_(rms)=\sqrt{(3RT)/(M)}` (1)

Where
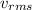`v_(rms)` is the root mean square velocity, M is the molar mass of the gas, R is the universal constant of the ideal gases and T is the temperature.

The root mean square velocity is a measure of the velocity of the particles in a gas. It is defined as the square root of the mean square velocity of the gas molecules:

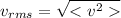`v_(rms)=√(<v^2>)` (2)

substituting 2 in 1, we find the relationship between mean square speed and temperature:

`√(<v^2>)=\sqrt{(3RT)/(M)}\\T=(M<v^2>)/(3R)\\\\T\sim  <v^2>`