Answer:
Cos x = 1 -
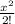 +
+
 -
-
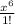 + ...
+ ...
Explanation:
We use Taylor series expansion to answer this question.
We have to find the expansion of cos x at x = 0
f(x) = cos x, f'(x) = -sin x, f''(x) = -cos x, f'''(x) = sin x, f''''(x) = cos x
Now we evaluate them at x = 0.
f(0) = 1, f'(0) = 0, f''(0) = -1, f'''(0) = 0, f''''(0) = 1
Now, by Taylor series expansion we have
f(x) = f(a) + f'(a)(x-a) +
 +
+
 +
+
 + ...
+ ...
Putting a = 0 and all the values from above in the expansion, we get,
Cos x = 1 -
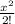 +
+
 -
-
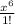 + ...
+ ...