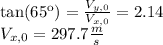Question

A football player punts the ball from the ground at a 65.0° angle above the horizontal. If the ball stays in the air for a total of 6.5 seconds, what are the vertical and horizontal components of the initial velocity?

Answer 1

Answer:
`V_(0,x ) = 297.7 (m)/(s)\\V_(0,y ) = 637 (m)/(s)`

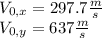
Step-by-step explanation:

Hi!

We define the point (0,0) as the intial position of the ball. The initial velocity is
`(V_(0,x), V_(0,y))`

The motion of the ball in the horizontal direction (x) has constant velocity, because there is no force in that direction. :

`x(t) = V_(0,x)t`

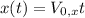
In the vertical direction (y), there is the downward acceleration g of gravity:

`y(t) = -gt^2 + V_(0,y)t`

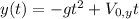
(note the minus sign of acceleration, because it points in the negative y-direction)

When the ball hits the ground, at t = 65s, y(t = 65 s) = 0. We use this to find the value of the initial vertical velocity:

`0 = t(-gt + V_(0,y))\\V_(0,y) = gt = 9.8 (m)/(s^2) 65 s = 637 (m)/(s)`

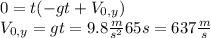
We used that g = 9.8 m/s²

To find the horizonttal component we use the angle:

`\tan(65\º) = (V_(y,0))/(V_(x,0)) = 2.14\\V_(x,0) = 297.7(m)/(s)`