Answer:
(a):
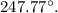
(b):
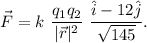
(c): Magnitude =

Sign = negative.
Step-by-step explanation:
(a):
Given that first charge is located at (3,-5) and second charge is located at (2,7).
The electrostatic force between two charges acts long the line joining the two charges, therefore, the direction of electrostatic force of attraction between these two charges is along the position vector of charge at (2,7) with respect to the position of charge at (3,-5).
Assuming,
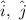 are the unit vectors along positive x and y axes respectively.
are the unit vectors along positive x and y axes respectively.
Position vector of charge at (3,-5) with respect to origin is

Position vector of charge at (2,7) with respect to origin is
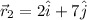
The position vector of at (2,7) with respect to the position of charge at (3,-5) is
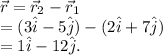
If
 is the angle this position vector is making with the positive x axis then,
is the angle this position vector is making with the positive x axis then,
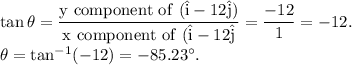
The negative sign indicates that this position vector is
 below the positive x axis, therefore, in counterclockwise direction from positive x axis, its direction =
below the positive x axis, therefore, in counterclockwise direction from positive x axis, its direction =

The force is also along the same direction.
(b):
According to Coulomb's law, the expression of this force is given by
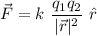
where,
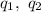 are the charges.
are the charges.
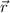 = position vector of one charge with respect to another charge.
= position vector of one charge with respect to another charge.
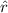 = unit vector along the direction of
= unit vector along the direction of
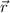 .
.
 = Coulomb's constant, which have value =
= Coulomb's constant, which have value =
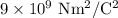 .
.
We have,
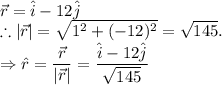
Putting this value, we get,
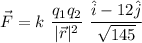
(c):
If charge at (3,-5) is
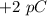 , then the magnitude of the force between the two charges is given by
, then the magnitude of the force between the two charges is given by

where, we have,
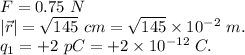
Putting all these values,
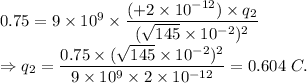
Since, the electric force between the two spheres is given to be attractive therefore this charge must be negative as the other charge is positive.