Answer with Explanation:
We know from newton's second law that acceleration produced by a force 'F' in a body of mass 'm' is given by
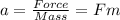
In the given case the acceleration equals
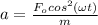
Now by definition of acceleration we have

Similarly by definition of position we have
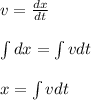
Upon further solving we get
![x=\int [(F_(o))/(\omega m)\cdot ((\omega t)/(2)+(sin(2\omega t))/(4)+c)]dt\\\\x=(F_(o))/(\omega m)\cdot ((\int (\omega t)/(2)+(sin(2\omega t))/(4)+c)dt)\\\\x(t)=(F_(o))/(\omega m)\cdot ((\omega t^(2))/(4)-(cos(2\omega t))/(8\omega )+ct+d)](https://img.qammunity.org/2020/formulas/physics/college/71uycd8lcdq9ie87c0gbsdwgg70xnr77qv.png)
The plots can be obtained depending upon the values of the constants.