Question

At Phill's Discount Car Kingdom, you can purchase a used car for $14,000. Phill offers you two payment options: Option 1: You can apply an immediate cash rebate of $2,000 from the dealer to reduce the cost of the car and finance the rest with a loan that has an annual rate of 3.6%, with interest compounded monthly, for 3 years. You would make equal payments at the end of each month until the loan was repaid . Option 2: You can take out a 0% loan for the full price of the car in which you agree to pay the same amount at the end of each month for 3 years until the car is paid off What is the total amount that you would pay (out of pocket) for the car under each option?

Answer 1

Ans. For option 1, you would pay a total of $14,677.64 and for the second option, you would pay $14,000.

Explanation:

Hi, we need to find the amount of the equal payments that you need to make every month, given the problem´s conditions. First, let´s find the effective montly rate of this credit.

`EffectiveMonthlyRate=(Rate(Compounded Monthly))/(12)`
`EffectiveMonthlyRate=(0.036)/(12) =0.003`

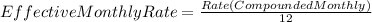
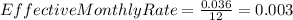
This means that the rate is 0.3% effective monthly

The period of time for this obligation is 3 years, but since the payments are made every month, we need to use 36 months instead of 3 years.

Now, we are ready to find the amount of money that you need to pay every month, for 36 months in order to pay for your car. We use the following formula.

`PresentValue=(A((1+r)^(n)-1) )/(r(1+r)^(n) )`

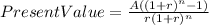
Since you made a down payment of $2,000, we will only need to finance $12,000. This is the way everything should look like.

`12,000=(A((1+0.003)^(36)-1) )/(0.003(1+0.003)^(36) )`

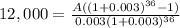
Let´s solve for A (annuity)

`12,000=(A(0.11386764 )/(0.003416 )`

`12,000==A(34.0757554)`}

`(12,000)/(34.0757554) =A=352.17`

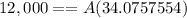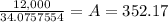
The total amount paid if you take this option is:

`Amount Paid=2,000+352.17*36=14,677.64`

In the case of option 2 (0% loan-pay same amount every month for 36 months), there is no need for any calculations (because you pay $14,000 in total), but if you want to know how much to pay every month, you just go ahead and divide 14,000 by 36 which is $388.89. But at the end, this way you will pay $14,000.

Best of luck.