Question

Ship A is located 3.90 km north and 2.50 km east of ship B. Ship A has a velocity of 21.0 km/h toward the south and ship B has a velocity of 40.0 km/h in a direction 37.0° north of east. What are the (a) x-component and (b) y-component of the velocity of A relative to B? (Axis directions are determined by the unit vectors i and j, where i is toward the east.) (c) At what time is the separation between the ships least? (d) What is that least separation?

Answer 1

a) Vx = -31.95 km/h b) Vy = -45.07 km/h

c) t = 0.083 h d) d = 0.22 km

Step-by-step explanation:

First we have to express these values as vectors:

ra = (2.5, 3.9) km rb = (0,0)km

Va = (0, - 21) km/h Vb = (31.95, 24.07) km/h

Now we can calculate relative velocity:

`V_(A/B) = V_(A) - V_(B) = (0, -21) - (31.95, 24.07) = (-31.95, -45.07) km/h`

For parts (c) and (d) we need the position of A relative to B and the module of the position will be de distance.

`r_(A/B) = (2.5, 3.9) + (-31.95, -45.07) * t`

`d = |r_(A/B)| = \sqrt{(2.5 -31.95*t)^(2)+(3.9-45.07*t)^(2)}`

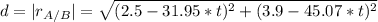
In order to find out the minimum distance we have to derive and find t where it equals zero:

`d' = \frac{-2*(2.5-31.95*t)*(-31.95)-2*(3.9-45.07*t)*(-45.07)}{2*\sqrt{(2.5 -31.95*t)^(2)+(3.9-45.07*t)^(2)}} =0`

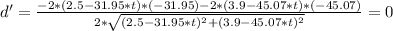
Solving for t we find:

t = 0.083 h

Replacing this value into equation for d:

d = 0.22 km