Question

How many strings of eight lower-case English letters are there that contain the two letters bg, in that order, with the further constraint that no letters can be repeated?

Answer 1

Answer: 678,363,840

Step-by-step explanation:

Hi!

The "bg" part of the string could be in 7 possible positions within the string. If we number the characters in the string from 0 to 7, the "b" of "bg" could be in positions 0 to 6.

We need to count the possibilities for the other 6 characters. They can be any of the 26 lower-case letters, but not b nor g, because no letters can be repeated. So we can choose 6 letters from 24 letters, without repetition, and the order is important. The number of such combinations is:

`n = 24,\; m = 6\\(n!)/((n-m)!) = (24!)/(18!) = 96,909,120`

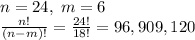
For the total number of strings, we have to multiply with the 7 possible position of "bg". Then, the final number is 678,363,840