Question

A 0.5 μF and a 11 μF capacitors are connected in series. Then the pair are connected in parallel with a 1.5 μF capacitor. What is the equivalent capacitance? Give answer in terms of mF.

Answer 1

`C_(eq)=1.97\ \mu F`

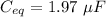
Step-by-step explanation:

Given that,

Capacitance 1,
`C_1=0.5\ \mu F`

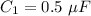
Capacitance 2,
`C_2=11\ \mu F`

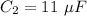
Capacitance 3,
`C_3=1.5\ \mu F`

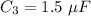
C₁ and C₂ are connected in series. Their equivalent is given by :

`(1)/(C')=(1)/(C_1)+(1)/(C_2)`

`(1)/(C')=(1)/(0.5)+(1)/(11)`

`C'=0.47\ \mu F`

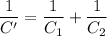
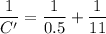
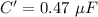
Now C' and C₃ are connected in parallel. So, the final equivalent capacitance is given by :

`C_(eq)=C'+C_3`

`C_(eq)=0.47+1.5`

`C_(eq)=1.97\ \mu F`

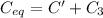
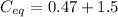
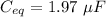
So, the equivalent capacitance of the combination is 1.97 micro farad. Hence, this is the required solution.