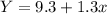Question

Consider the following data points.

P1(1, 3), P2(2, 4), P3(3, 5), P4(4, 7), P5(5, 8)

(a) Find the equation of the least-squares line for the data.
y(x) =

Answer 1

y= 9.3 1.3

Explanation:

Answer 2

the equation of the least-squares line for the data is:
`\hat Y=9.3+1.3x`

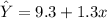
Explanation:

In a simple linear regression model, such as,
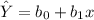`\hat Y=b_0+b_1x`, the coefficients bo and b1 are estimated through the method of least squares by the use of the equations:

`b_1=\frac{S{xy}}{S_x^2}\\\\b_0=\bar{y}+b_1 \bar{x}`

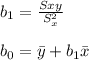
For the data provided you have to:

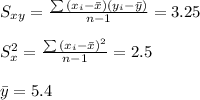`S_(xy)=\frac{\sum {(x_i-\bar x)(y_i-\bar y)}}{n-1}=3.25\\\\S_x^2=\frac{\sum {(x_i-\bar x)^2}}{n-1}=2.5\\\\\bar y=5.4`, thus:

`b_1=(3.25)/(2,5)=1.3\\\\b_0=5.4+1.3(3.0)=9.3`

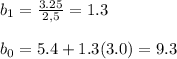
the equation of the least-squares line for the data is:

`Y=9.3+1.3x`