Question

A rose garden can be planted for $4000. The marginal cost of growing a rose is estimated to $0.30,

and the total revenue from selling 500 roses is estimated to $875. Write down the equations for

the Cost (5pts), Revenue (5pts) and Profit (5pts) functions and graph them all in the same

coordinate axes (30 pts). What is the break-even quantity? (5pt

Answer 1

`C(x)=4000+0.3x`

`R(x)=1.75x`

`Profit= 1.45x-4000`

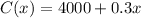
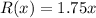
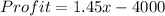
Explanation:

We are given that A rose garden can be planted for $4000.

The marginal cost of growing a rose is estimated to $0.30,

Let x be the number of roses

So, Marginal cost of growing x roses =
`0.3x`

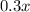
Total cost =
`4000+0.3x`

So, Cost function :
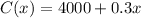`C(x)=4000+0.3x` ---A

Now we are given that the total revenue from selling 500 roses is estimated to $875

So, Marginal revenue =
`\frac{\text{Total revenue}}{\text{No. of roses}}`

Marginal revenue =
`(875)/(500)`

Marginal revenue =
`1.75`

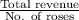
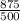
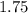
Marginal revenue for x roses =
`1.75x`

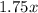
So, Revenue function =
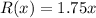`R(x)=1.75x` ----B

Profit = Revenue - Cost

`Profit= 1.75x-4000-0.3x`

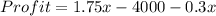
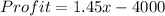`Profit= 1.45x-4000` ---C

Now Plot A , B and C on Graph

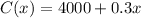`C(x)=4000+0.3x` -- Green

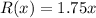`R(x)=1.75x` -- Purple

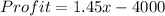`Profit= 1.45x-4000` --- Black

Refer the attached graph