Question

Use the work-energy theorem to determine the force required to stop a 1000 kg car moving at a speed of 20.0 m/s if there is a distance of 45.0 m in which to stop it.

Answer 1

4.44 kN in the opposite direction of acceleration.

Step-by-step explanation:

Given that, the initial speed of the car is,
`u=20m/s`

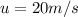
And the mass of the car is,
`m=1000 kg`

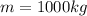
The total distance covered by the car before stop,
`s=45m`

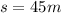
And the final speed of the car is,
`u=0m/s`

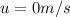
Now initial kinetic energy is,

`KE_(i)=(1)/(2)mu^(2)`

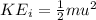
Substitute the value of u and m in the above equation, we get

`KE_(i)=(1)/(2)(1000kg)* (20)^(2)\\KE_(i)=20000J`

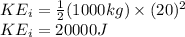
Now final kinetic energy is,

`KE_(f)=(1)/(2)mv^(2)`

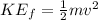
Substitute the value of v and m in the above equation, we get

`KE_(f)=(1)/(2)(1000kg)* (0)^(2)\\KE_(i)=0J`

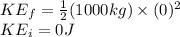
Now applying work energy theorem.

Work done= change in kinetic energy

Therefore,

`F.S=KE_(f)-KE_(i)\\F* 45=(0-200000)J\\F=(-200000J)/(45)\\ F=-4444.44N\\F=-4.44kN`

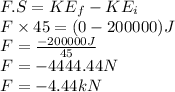
Here, the force is negative because the force and acceleration in the opposite direction.