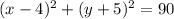Question

Find an equation of the circle that satisfies the given conditions. (Give your answer in terms of x and y.)

Center

(4, −5)

and passes through

(7, 4)

Answer 1

`(x-4)^2+(y+5)^2=90`

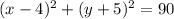
Explanation:

The equation of a circle of radius r, centered at the point (a,b) is

`(x-a)^2+(y-b)^2=r^2`

We already know the center is at
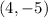`(4,-5)`, we are just missing the radius. To find the radius, we can use the fact that the circle passes through the point (7,4), and so the radius is just the distance from the center to this point (see attached image). So we find the distance by using distance formula between the points (7,4) and (4,-5):

radius
`=√((7-4)^2+(4-(-5))^2)=√(3^2+9^2)=√(90)`

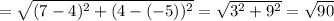
And now that we know the radius, we can write the equation of the circle:

`(x-4)^2+(y-(-5))^2=√(90)^2`

`(x-4)^2+(y+5)^2=90`