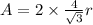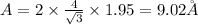Answer:
(a) A =

(b)
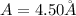
(c)
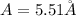
(d)

Solution:
As per the question:
Radius of atom, r = 1.95
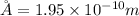
Now,
(a) For a simple cubic lattice, lattice constant A:
A = 2r
A =
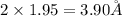
(b) For body centered cubic lattice:
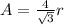
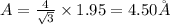
(c) For face centered cubic lattice:

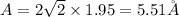
(d) For diamond lattice: